温泉玉子装置の評価
玉子と水のエネルギー方程式の解析解を求め,容器やヒータ容量を評価する.
1. 支配方程式
1.1 エネルギー方程式
玉子内の熱移動を一次元熱伝導として以下の仮定の下,支配方程式を導く.
【仮定】
(i). 玉子を球形とする.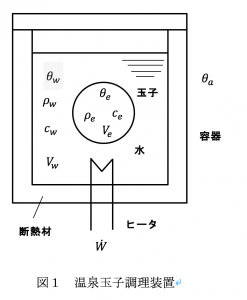
(ii). 容器内の水は対流により撹拌され,温度分布は無視できる状態になっている.
(iii). 玉子表面と容器表面の熱伝達率は,位置および温度に依存しない定数とする.
(iv). 玉子の密度と熱伝導率は白身と黄身の区別なく一様であり,温度に依存しない定数とする.
(v). 玉子の体積を二等分する半径上の温度を代表温度とする.
(vi). 玉子の質量は,この代表温度半径上の球面に集中しているとする.
(vii). 玉子および水の物性値は,温度に依存しない定数とする.
仮定(ⅱ)と(ⅵ)から集中定数系としてモデル化する.また,仮定(ⅰ),(ⅱ),(ⅲ),(ⅳ)から,玉子内の温度勾配は半径方向にのみ生じる.ここで,玉子には熱の出入りがあるだけで仕事はなされないが,水には熱入力のほかに電気的仕事が作用する.そこでこれらを考慮すると,付録の式(A7)から玉子および水のエネルギー方程式はそれぞれ次式で与えられる.
\begin{eqnarray}
&c_{e}&\rho_{e}V_{e} \frac{d\theta_{e}}{dt} = \dot{Q}_{we} …(1)\\
&c_{w}&\rho_{w}V_{w} \frac{d\theta_{w}}{dt} = \dot{Q}_{ew}+\dot{Q}_{aw}+\dot{W}…(2)
\end{eqnarray}
ただし、 c: 比熱(J/(kg・K))\(\dot{Q}\):熱流(W) t:時間(s) V:容積(m3)\(\dot{W}\):ヒータ入力(W)\(\theta\) :温度(℃)\(\rho\):密度(kg/m3)
添え字 a:外気 c:容器 e:玉子 w:水 aw:外気から水へ ew:玉子から水へ we:水から玉子へ
なお,式(A7)では比熱は定積比熱であるが,液体の場合は定圧比熱と定積比熱はほぼ等しいのでこれを区別せず cとした(1).また,式(1)の右辺は水から玉子への熱流,式(2)の右辺第一項,第二項はそれぞれ玉子から水へ,外気から水への熱流,第三項はヒータ入力である.
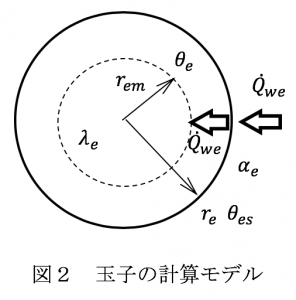
式(1)右辺の水から玉子への熱流は,水から玉子表面への熱伝達,玉子表面から代表温度半径 \(r_{em}\)までの熱伝導に分けて考えることができるが,仮定(ⅵ)からこの間の玉子には質量は無く,熱流を蓄える部分が存在しないので,これらの熱流の値は等しくなる.
水から玉子表面への熱流は,玉子表面の熱伝達率を \(a_e\)とすれば
\begin{eqnarray} \dot{Q}_{we} = 4\pi r_{e}^{2}\alpha_{e}(\theta_{w}-\theta_{es}) \end{eqnarray} 玉子表面から代表温度半径までの熱流は,付録の式(B5)が半径増加方向の熱流を正とした式であるので,この式の温度差の項の順序を入替えて玉子に流入する熱流を正とすると \begin{eqnarray} \dot{Q}_{we} = \frac{4\pi \lambda_{e}}{\displaystyle\frac{1}{r_{em}}-\frac{1}{r_{e}}}(\theta_{es}-\theta_{e}) \end{eqnarray}
式(3),(4)から
\begin{eqnarray*} \frac{\dot{Q}_{we}}{4\pi r_{e}^{2}\alpha_{e}}=\theta_{w}-\theta{es}…(3′) \end{eqnarray*}
\begin{eqnarray*} \frac{\displaystyle\frac{1}{r_{em}}-\frac{1}{r_{e}}}{4\pi \lambda_{e}}\dot{Q}_{we}=\theta_{es}-\theta{e}…(4′) \end{eqnarray*}
式(3′)と(4′)を辺々加え合わせて玉子表面温度\(\theta_{es}\)を消去し整理すると \begin{eqnarray} \dot{Q}_{we} &=& \frac{1}{\displaystyle\frac{r_{e}-r_{em}}{4\pi \lambda_{e}r_{e}r_{em}}+\frac{1} {4\pi r_{e}^{2}\alpha_{e}}} (\theta_{w}-\theta_{e}) \nonumber \\ &=& K A_{e}(\theta_{w}-\theta_{e}) \end{eqnarray} ただし,式(5)右辺一行目の温度差の係数を\(KA_{e}\)と置いた. 一方,水は\(dot{Q}_{we}\)なる熱量を玉子に与えるのでこれに等しい熱量を失う.よって \begin{equation} \dot{Q}_{ew} = -\dot{Q}_{we} \end{equation} なお代表温度半径は,仮定(e)から
\[ \frac{4}{3}\pi r_{em}^{3}=\frac{1}{2} \left( \frac{4}{3 }\pi r_{e}^{3} \right) \] \begin{equation} ∴r_{em}=\frac{1}{\sqrt[3]{2}} r_{e} \end{equation} ここで \(r\):半径(m) \(\alpha\):熱伝達率(W/(m\(^{2}\)・K)) \(\lambda\):熱伝導率(W/(m・K))
添え字 \(e\):玉子 \(em\):代表 \(es\):表面
1.3 外気から水への熱流
外気から円筒容器側面外側への熱流は,側壁高さ\(h_{c}\),外半径を\(r_{co}\)とすれば \begin{equation} \dot{Q}_{c}=2\pi r_{co} h_{c}\alpha_{a}(\theta_{a}-\theta_{co}) \end{equation} 容器側面外側から内側への熱流は式(4)と同様に,付録の式(B3)の温度差の順序を入替え,壁の熱伝導率を\(\lambda_{c}\),内半径を\(r_{ci}\)とすると \begin{equation} \dot{Q}_{c}=\frac{2\pi h_{c} \lambda_{c}}{\ln(r_{co}/r_{ci})} (\theta_{co}-\theta_{ci}) \end{equation}容器側面内側から水への熱流は \begin{equation} \dot{Q}_{c}= 2\pi r_{ci} h_{c}\alpha_{w}(\theta_{ci}-\theta_{w}) \end{equation} 式(8),(9),(10)から
\begin{eqnarray*} \frac{\dot{Q}_{c}}{2\pi r_{co}h_{c}\alpha_{a}}=\theta_{a}-\theta_{co}…(8′)\end{eqnarray*}
\begin{eqnarray*} \frac{\ln(r_{co}/r_{ci})}{2\pi h_{c} \lambda_{c}}\dot{Q}_{c}=\theta_{co}-\theta_{ci}…(9′) \end{eqnarray*}
\begin{eqnarray*} \frac{\dot{Q}_{c}}{2\pi r_{ci} h_{c}\alpha_{w}}=\theta_{ci}-\theta_{w}…(10′) \end{eqnarray*}
式(8′),(9′),(10′)を辺々加え合わせて整理すると,側壁を通過して流入する熱量\(\dot{Q}_{c}\)は
\begin{equation} \dot{Q}_{c}=\frac{1}{\displaystyle\frac{1}{2\pi r_{co}h_{c}\alpha_{a}}+\frac{\ln(r_{co}/r_{ci})}{2\pi h_{c} \lambda_{c}}+\frac{1}{2\pi r_{ci} h_{c}\alpha_{w}}}(\theta_{a}-\theta_{w}) \end{equation}
底面の面積を\(A_{b}\)とすれば,同様に外気から容器底面外側への熱流は
\begin{equation} \dot{Q}_{b}=A_{b}\alpha_{a}(\theta_{a}-\theta_{bo}) \end{equation} 容器底面外側から内側への熱流は,底面の熱伝導率を\(\lambda_{b}\),厚さを\(\delta_{b}\)とすれば \begin{equation} \dot{Q}_{b}=A_{b}\frac{\lambda_{b}}{\delta_{b}}(\theta_{bo}-\theta_{bi}) \end{equation} 容器底面から水への熱流は \begin{equation} \dot{Q}_{b}=A_{b}\alpha_{w}(\theta_{bi}-\theta_{w}) \end{equation} 側面と同様に底面を通過して流入する熱量\(\dot{Q}_{b}\)は \begin{eqnarray} \dot{Q}_{b}&=&\frac{1}{\displaystyle\frac{1}{A_{b}\alpha_{a}}+\frac{\delta_{b}}{A_{b} \lambda_{b}}+\frac{1}{A_{b} \alpha_{w}}}(\theta_{a}-\theta_{w}) \nonumber \\ &=&\frac{A_{b}}{\displaystyle\frac{1}{\alpha_{a}}+\frac{\delta_{b}}{ \lambda_{b}}+\frac{1}{\alpha_{w}}}(\theta_{a}-\theta_{w}) \end{eqnarray} 外気からの熱流は\(dot{Q}_{c}\)と\(\dot{Q}_{b}\)の和であるので,式(2)の右辺第二項は式(11)と式(15)から \begin{eqnarray} \dot{Q}_{aw}&=&\dot{Q}_{c}+\dot{Q}_{b} \nonumber \\ &=&\left [\frac{1}{\displaystyle\frac{1}{2\pi r_{co}h_{c}\alpha_{a}}+\frac{\ln(r_{co}/r_{ci})}{2\pi h_{c} \lambda_{c}}+\frac{1}{2\pi r_{ci} h_{c}\alpha_{w}}} \right. \nonumber \\ & + & \left. \frac{A_{b}}{\displaystyle\frac{1}{\alpha_{a}}+\frac{\delta_{b}}{\lambda_{b}}+\frac{1}{\alpha_{w}}} \right] (\theta_{a}-\theta_{w}) \nonumber \\ &=&KA_{c}(\theta_{a}-\theta_{w}) \end{eqnarray} ただし,式(16)右辺二行目の温度差の係数を\(KA_{c}\)と置いた.
ここで \(A\):伝熱面積(m\(^2\)) \(h\):高さ(m)
\(KA\):熱通過係数(W/K) \(r\):半径(m) \(\alpha\):熱伝達率(W/(\(m^2\)・K))
\(\lambda\):熱伝導率(W/(m・K)) \(\delta\):厚さ(m)
添え字 \(a\):外気 \(b\):底面 \(c\):容器 \(w\):水 \(aw\):外気から水 \(ci\):容器内側 \(co\):容器外側
2 支配方程式の解析解
仮定(c),(d),(g)から式(1),(2)の係数は定数となるので解析解を求めることができる.
2.1 玉子の温度と水温が同時に変化する場合
式(1),(2)に式(5),(6)および(16)を代入して整理すると
\begin{eqnarray*} \frac{d\theta_{e}}{dt}=\frac{KA_{e}}{c_{e}\rho_{e}V_{e}}(\theta_{w}-\theta_{e})…(1′) \end{eqnarray*}
\begin{eqnarray*} \frac{d\theta_{w}}{dt} &=& \frac{KA_{e}}{c_{w}\rho_{w}V_{w}}(\theta_{e}-\theta_{w})+\frac{KA_{c}}{c_{w}\rho_{w}V_{w}}(\theta_{a}-\theta_{w}) \\ &+& \frac{\dot{W}}{c_{w}\rho_{w}V_{w}}…(2′) \end{eqnarray*}
ここで \[ D=\frac{d}{dt} A=\frac{KA_{e}}{c_{e}\rho_{e}V_{e}} B=\frac{KA_{e}}{c_{w}\rho_{w}V_{w}} \] \[ C=\frac{KA_{c}}{c_{w}\rho_{w}V_{w}} E=\frac{\dot{W}}{c_{w}\rho_{w}V_{w}} \] と置き整理すると次式を得る. \begin{eqnarray} (&D&+A)\theta_{e} = A\theta_{w} \\ (&D&+F)\theta_{w} = B\theta_{e}+C\theta_{a}+E \end{eqnarray} ただし \(F=B+C\) であり,また仮定(c),(d),(g)から\(A, B, C, E\)は定数となる.
式(17)の両辺に \((D+F)\) を作用させ,その右辺に式(18)を代入すると \begin{eqnarray*} (D+F)(D+A)&\theta_{e}& = A(D+F)\theta_{w} \nonumber \\ &=& A(B\theta_{e}+C\theta_{a}+E) \end{eqnarray*} \(\theta_{e}\)に関し整理すると \begin{eqnarray} \{D^2+(A+F)D+AF&-&AB\} \theta{e} \nonumber \\ &=&AC\theta{a}+AE \end{eqnarray} 式(19)左辺の演算子多項式を因数分解して \begin{eqnarray*} (D-\alpha)(D-\beta)\theta_{e}=AC\theta_{a}+AE (19′) \end{eqnarray*} \(\alpha,\beta\) は補助方程式\(x^2+(A+F)x+AF-AB=0\) の解であり次式で与えられる. \begin{eqnarray*} \alpha&=&\frac{-(A+F)+\sqrt{(A+F)^2-4(AF-AB)}}{2} \\ \beta&=&\frac{-(A+F)-\sqrt{(A+F)^2-4(AF-AB)}}{2} \end{eqnarray*}
ここで \((A+F)^2-4(AF-AB)=(A-F)^2+4AB>0\)であるから\(\alpha,\beta\)は実根である. よって式(19′)の斉次方程式 \((D-\alpha)(D-\beta)=0\) の一般解は\(a,b\)を任意定数として
\( \theta_{e}=ae^{\alpha t}+be^{\beta t} \)
なお\( \sqrt{(A+F)^2-4(AF-AB)} \) =\( \sqrt{(A+F)^2-4AC} \) \(<(A+F)\) であるから\(\alpha<0,\beta<0\)である. 式(19)の特殊解は山辺の方法\(^{(2)}\)により,以下示すように演算子多項式を除式とみなし,数式の割り算形式で求めることができる.
すなわち特殊解は \[ \theta_{e}=(AC\theta_{a}+AE)/AC=(C\theta_{a}+E)/C \] 特殊解と斉次方程式の一般解の和が線形微分方程式の一般解である\(^{(2)}\)から,式(19)の一般解は \begin{equation} \theta_{e}=a\mathrm{e}^{\alpha t}+b\mathrm{e}^{\beta t}+(C\theta_{a}+E)/C \end{equation} 式(17)に式(21)を代入して整理すると \begin{eqnarray} \theta_{w} &=& \frac{1}{A}(D+A)\theta_{e}=\frac{1}{A}\frac{d\theta_{e}}{dt}+\theta_{e} \nonumber \\ &=& \frac{a(A+\alpha)}{A}\mathrm{e}_{\alpha t} + \frac{b(A+\beta)}{A}\mathrm{e}_{\beta t} \nonumber \\ &+& \frac{C\theta_{a}+E}{C} \end{eqnarray} 式(21),(22)に初期条件\(t=0,~ \theta_{e}=\theta_{e0},~ \theta_{w}=\theta_{w0}\)を適用すると \[ \theta_{e0}=a+b+(C\theta_{a}+E)/C~~ (21′) \] \begin{eqnarray*} \theta_{w0}&=& \frac{a(A+\alpha)}{A} + \frac{b(A+\beta)}{A} \\ &+& \frac{C\theta_{a}+E}{C} (22′) \end{eqnarray*}
式(21′)と(22′)を任意定数\(a,~b\)について解いて \begin{eqnarray} a&=& \frac{-(A+\beta)}{\alpha-\beta}\theta_{e0} + \frac{A}{\alpha-\beta}\theta_{w0} \nonumber \\ &+& \frac{\beta}{\alpha-\beta}\frac{C\theta_{a}+E}{C} \\ b&=& \frac{A+\alpha}{\alpha-\beta}\theta_{e0} – \frac{A}{\alpha-\beta}\theta_{w0} \nonumber \\ &-& \frac{\alpha}{\alpha-\beta}\frac{C\theta_{a}+E}{C} \end{eqnarray}
2.2 水温一定場合
水温が上昇し所定の温度に達すると,この温度を維持するように水温が制御されるので\(\theta_{e}\)のみ変化し\(\theta_{w}\)は定数となる.そこでこの場合は式(1)のみを解けばよい.
式(17)の斉次方程式の一般解は \[ \theta_{e}=a\mathrm{e}^{-At} \] 式(17)の特殊解は山辺の方法により
よって式(1)の一般解は \[ \theta_{e}=a\mathrm{e}^{-At}+\theta_{w} \] 初期条件\( t=0,~ \theta_{e}=\theta_{e0} \)から\(a=\theta_{e0}-\theta_{w}\)を得る. \begin{equation} ∴ ~\theta_{e}=(\theta_{e0}-\theta_{w})\mathrm{e}^{-At}+\theta_{w} \end{equation}
3 試算例
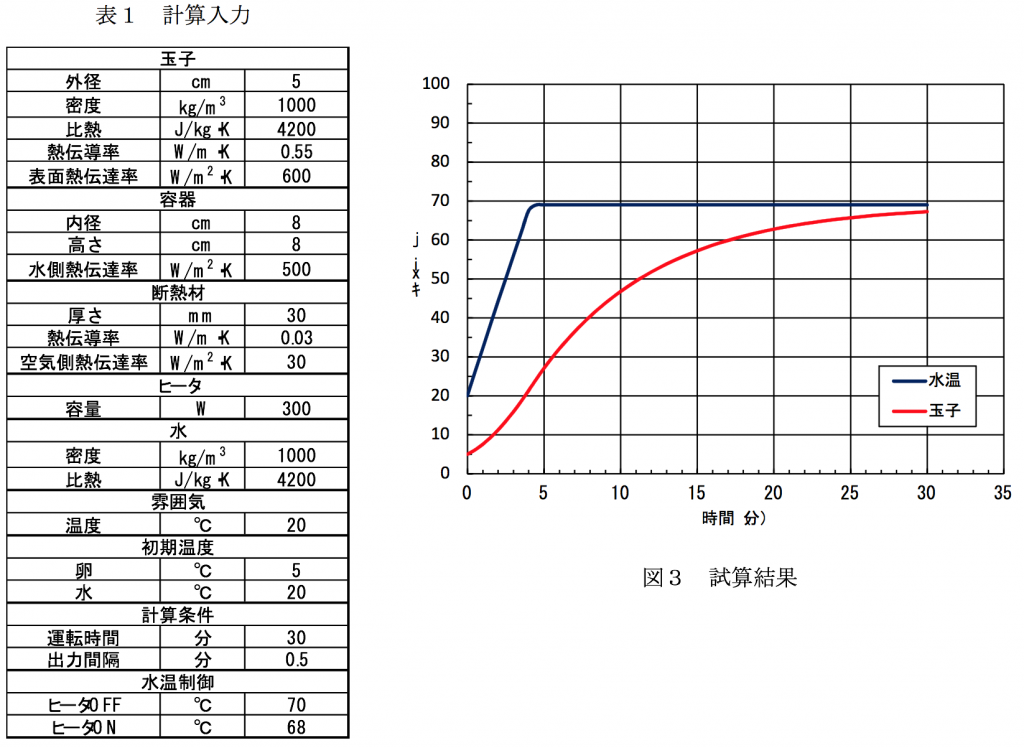
式(21),(22)に,表1に示す具体的数値を適用して計算した結果を示す.計算式が煩雑であるのでエクセルVBAを使用して計算した.ヒータ OFF 70℃,ヒータON 68℃としたので,設定水温を69℃として計算する.水温が69℃に達した時点で水温を一定として,以後式(25)を使用して玉子の温度を計算する.なお,水温が69℃に達した時点を式(25)の初期時刻\(t=0\)とし,このときの玉子の温度を初期温度\(\theta_{e0}\)とした.
加熱開始直後の水温が上昇する時間帯では,水と玉子との温度差が大きくとれるので玉子の温度も大きく上昇するが,水温が一定になると玉子の温度が上昇するに従い水との温度差が減少し,玉子の温度上昇割合も小さくなる.そこで,所定の時間内に玉子の温度を所定の温度まで上昇させるには,なるべく短時間で水温を設定温度まで上昇させ,水温一定で加熱する時間を長くする必要がる.なお,断熱材厚さ変えて計算した結果,断熱材厚さは水温上昇にほとんど影響を与えないことがわかった.
付録
A. エネルギー方程式
A.1 熱力学第1法則
熱力学第1法則によれば,系の内部エネルギーの増加は加えられた熱量と,外部からなされた仕事量の和に等しい\(^{(3)}\)ので \[ dU=\delta Q+\delta W (\rm{A}1) \] ここで \(U\):内部エネルギー(J) \(Q\):熱量(J)\\ \(W\):仕事量(J)\\ または単位質量あたり \[ du=\delta q+\delta w (A2) \] \(u\):比内部エネルギー(J/kg) \(q\):熱量(J/kg) \(w\):仕事量(J/kg)
なお内部エネルギーは,圧力や温度の状態により一意に定まる”状態量”であるが,熱や仕事は系 に”作用”する量であり値は変化の過程に依存する.そこで状態量の微小変化は全微分となる\(^{(4)}\)ことを考慮して\(d\)で表し,熱量や仕事の変化は単なる増分であるので\(\delta\)で表記した.
A.2 比熱と内部エネルギーの関係
外部からなされる仕事が系の体積変化にのみ起因する場合,体積変化を\(dv\),外界の圧力を\(p\)とすると\(p\)は常に系の体積が減少する方向に作用する.そこで\(dv>0\)のとき圧力の作用する方向と体積の変化する方向は逆向きとなり,圧力がなす仕事は負となる.すなわち式(A2)における外部からなされた仕事は\(\delta w = -pdv\)(\(p\)の値は常に正である)\(^{(4)}\)となる.よって式(A2)から \[ du=\delta q – pdv (\rm{A}2′) \] 体積を一定に保ちながら加熱する場合は\(dv=0\)であるので定積比熱\(c_{v}\) (J/(kg・K))は \[ c_{v}=\left(\frac{\delta q}{\partial \theta}\right)_{v} = \left(\frac{\partial u}{\partial \theta}\right)_{v} (\rm{A}3) \] ここで右辺の添え字\(v\)は体積を一定とした偏微分を意味する.理想気体や液体の場合,内部エネルギーは温度のみの関数になる\(^{(1)}\)ので \[ c_{v}=\frac{du}{d \theta}~ (\rm{A}4) \]
A.3 エネルギー方程式(内部エネルギーが温度のみの関数の場合)
密度\(\rho\)(kg/m\(^{3}\)),容積\(V\)(m\(^{3}\))の系の内部エネルギーは\(U=\rho Vu\)であるので式(A1)から \[ d(\rho Vu) = \delta Q+\delta W~ (\rm{A}5) \] さらに\(dt\)秒で式(A5)の変化が生じたとすると単位時間当たりの変化は \[ \frac{d}{dt}(\rho Vu) = \dot Q+\dot W~ (\rm{A}6) \] ただし\(\dot Q\)(J/s=W)および\(\dot W\)(J/s=W)は単位時間当たりの増分である.
ここで容積\(V\)は変化せず,また密度\(\rho\)の変化も無視でき,さらに内部エネルギーが温度のみの関数の場合,式(A4)を考慮して式(A6)の左辺を変形すると \[ \frac{d}{dt}(\rho Vu) = \rho V\frac{du}{dt}=\rho V\frac{du}{d\theta}\frac{d\theta}{dt}=c_{v}\rho V\frac{d\theta}{dt} \]
よって系のエネルギー方程式は \[ c_{v}\rho V\frac{d\theta}{dt} = \dot Q+\dot W (\rm{A}7) \] となる.
参考
系に質量の出入りがある場合,内部エネルギーの出入りと圧力による排除仕事を伴うのでこれらを式(A7)右辺に考慮すると \begin{eqnarray*} c_{v}\rho V\frac{d\theta}{dt} &=& u_{i}G_{i}-u_{o}G_{o}+ p_{i}F_{i}w_{i}-p_{o}F_{o}w_{o} \\ &+& \dot Q+\dot W (\rm{A}8) \end{eqnarray*} ここで系の運動エネルギーと位置エネルギーの変化は無視した.さらに\(G=Fw/v\)であることを考慮して式(A8)の右辺を整理すると \begin{eqnarray*} c_{v}\rho V\frac{d\theta}{dt} &=& (u_{i}+ p_{i}v_{i})G_{i}-(u_{o}+p_{o}v_{o})G_{o} \\ &+& \dot Q+\dot W~ (\rm{A}9) \end{eqnarray*} また比エンタルピーは\(h=u+pv\)で定義されるので \[ c_{v}\rho V\frac{d\theta}{dt} =h_{i}G_{i}-h_{o}G_{o}+ \dot Q+\dot W~ (\rm{A}10) \]
ここで\(F\):流路断面積(m\(^2)\) G :質量流量(kg/s) h:比エンタルピー(J/kg) \(p\):圧力(Pa) \(v\):比容積(m\(^3\)/kg) \(w\):流速(m/s)
添え字 \(i\):流入 \(o\):流出
B. 円筒および球の半径\(r\)方向熱伝導\(^{(5)}\)
B.1 円筒
円筒が十分に長いか,両端が完全に断熱されている場合には円筒内の熱流は半径方向にのみ生じ,一次元熱伝導として取り扱える.フーリエの熱伝導の法則から円筒半径\(r\)方向の一次元熱伝導方程式は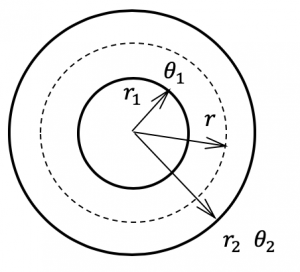 \[ \dot q=-\lambda \frac{d\theta}{dr} (\rm{B}1) \] ここで \(\dot q\):熱流束(単位時間に単位面積を通過する熱量)(J/(s・m\(^2\))=W/m\(^2\)) \(\theta\):温度(℃)\(\lambda\):熱伝導率(W/(m・K))
\[ \dot q=-\lambda \frac{d\theta}{dr} (\rm{B}1) \] ここで \(\dot q\):熱流束(単位時間に単位面積を通過する熱量)(J/(s・m\(^2\))=W/m\(^2\)) \(\theta\):温度(℃)\(\lambda\):熱伝導率(W/(m・K))
なお,温度勾配\((d\theta/dr)\)と熱の流れ方向の正負が逆であるので,\(r\)の増加する方向に流れる熱量が正となるように式(B1)右辺に負号を付けてある.
すなわち\(r\)の増加する方向に熱が流れる場合,温度はこの方向に減少\((d\theta/dr<0)\)しているので,負号によりこの熱流は正となる.
半径\(r\)(m),長さ\(l\)(m)の円柱面を通過する熱流を\(\dot Q\)とすると単位面積を通過する熱流は \[ \dot q=\frac{\dot Q}{2\pi rl} (\rm{B}2) \] 式(B1),(B2)から \[ d\theta=-\frac{\dot Q}{2\pi l\lambda}\frac{dr}{r} \] \(r=r_{1}\)で\(\theta=\theta_{1}\)なる境界条件の下で積分すれば \[ \theta=\theta_{1}-\frac{\dot Q}{2\pi l\lambda}\ln\frac{r}{r_{1}} \] \(r=r_{2}\)で\(\theta=\theta_{2}\)であるので,これを上式に代入し整理すれば \[ \dot Q=\frac{2\pi l\lambda}{\ln(r_{2}/r_{1})}(\theta_{1}-\theta_{2}) (\rm{B}3) \] B.2 球殻
球表面上に温度分布が存在しない場合,熱流は半径方向にのみ生じるので一次元熱伝導として取り扱うことができる.半径\(r\)の球面を通過する熱流を\(\dot Q\)とすれば熱流束\(\dot q\)は \[ \dot q=\frac{\dot Q}{4\pi r^2} (\rm{B}4) \] 式(B1),(B4)から \[ d\theta=-\frac{\dot Q}{4\pi \lambda}\frac{dr}{r^2} \] \(r=r_{1}\)で\(\theta=\theta_{1}\)なる境界条件の下で積分すれば \[ \theta=\theta_{1}+\frac{\dot Q}{4\pi \lambda}\left(\frac{1}{r}-\frac{1}{r_{1}}\right) \] \(r=r_{2}\)で\(\theta=\theta_{2}\)であるので,これを上式に代入し整理すれば \[ \dot Q=\frac{4\pi\lambda}{\displaystyle\frac{1}{r_{1}}-\frac{1}{r_{2}}}(\theta_{1}-\theta_{2}) (\rm{B}5) \]
文献
(1) 菅原菅雄,改訂 工業熱力学,(1976),P.111,岩波全書
(2) 矢野健太郎,石原 繁,解析学概論,(1966),P.41-71,裳華房
(3) 甲藤好郎,工学技術者のための熱力学,(2002),P.15,養賢堂
(4) 原島 鮮,熱力学・統計力学,(1972),P14,P18,培風館
(5) 相原利雄,伝熱工学,(2003),P.19,裳華房

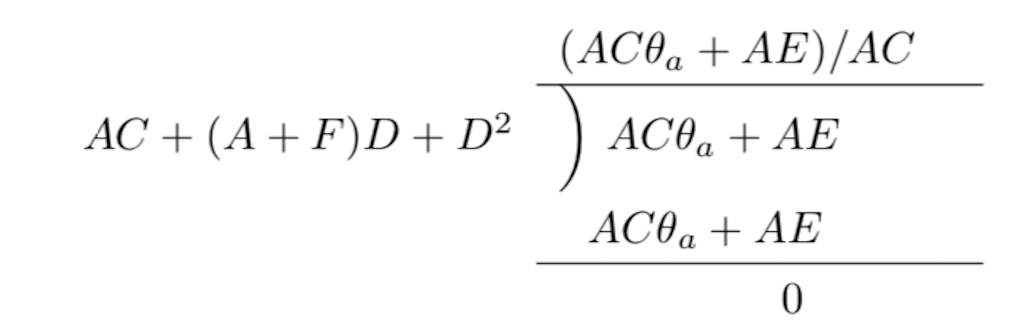
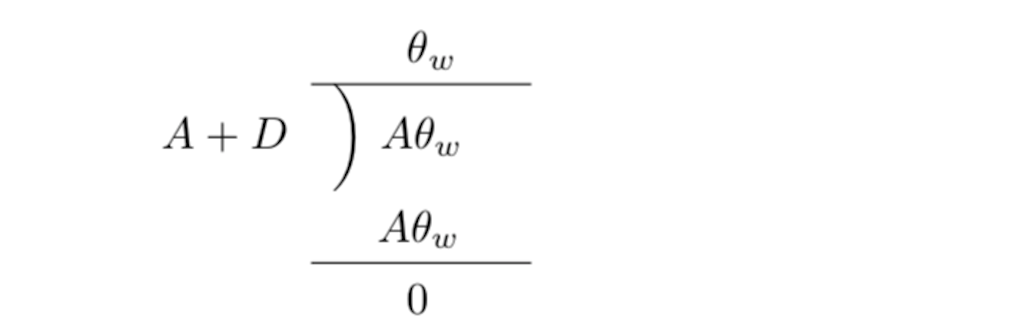
1件の返信
[…] https://shibaura-it.tokyo/technique/温泉玉子装置の評価/ […]